
츄르사려고 코딩하는 코집사입니다.
1. 엔트로피(Entropy)
머신러닝(Machine Learning)에서 자주 들어보는 단어 중 하나이다.
엔트로피는 불순도를 수치화한 지표 중 하나이며, 확률 변수의 불확실성을 수치로 나타낸 것이다. 또한, 정보량의 기댓값이라고 할 수 있다. 이 불순도를 수치화한 지표는 엔트로피, 지니계수 등이 있다.
우리가 의사결정나무(Decision Tree)를 시각화하면 의사결정나무의 노드에 entropy라는 것을 볼 수 있는데, 이 entropy의 값에 따라 의사결정나무(Decision Tree)의 분류가 일어나는 것을 확인할 수 있다. 아래의 사진을 보면 각 노드에 entropy가 존재하는 것을 볼 수 있다.
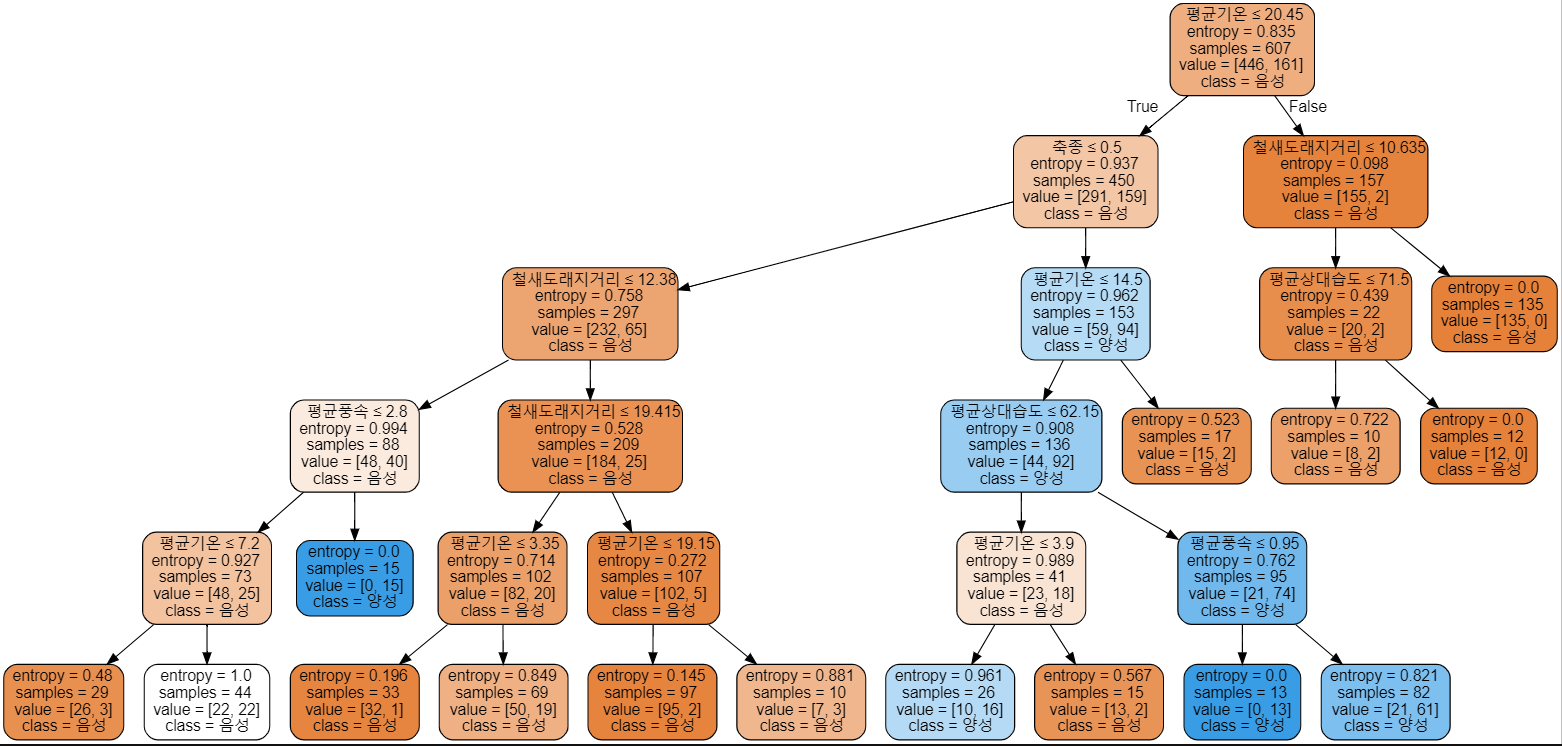
이 엔트로피(Entropy) 수치의 의미는 아래와 같다.
1) 엔트로피(Entropy) 수치가 0일 경우
- 해당 분류에 속하는 개체의 속성이 모두 동일하다. 즉, 분류를 하지 않아도 된다.
2) 엔트로피(Entropy) 수치가 1에 가까울 경우
- 불순도가 높다.
3) 엔트로피(Entropy) 수치가 0에 가까울 경우
- 불순도가 낮다.

아래의 그림에는 A, B, C의 이름을 가진 상자가 있다.
A 상자에는 빨간공 10개와 파란공 2개.
B 상자에는 파란공 12개.
C 상자에는 빨간공 6개와 파란공 6개.
B상자에서는 파란공이 12개가 있어 분류를 하지 않아도 되는 상황이라 엔트로피의 수치는 0이다.
C상자에서는 빨간공 6개와 파란공 6개로 공이 반반씩 섞여 있을 때 분류를 하기 힘들어져 엔트로피 수치는 최대가 된다.
반면에, A상자는 빨간공 10개와 파란공 2개를 분리해야 하므로, 엔트로피 수치는 C보다 낮다.
즉, 불순한 상태는 분류하기 어려운 상태로 볼 수 있으며 불순한 상태일 수록 엔트로피(Entropy)의 수치는 커지며, 불순도가 높을수록 분류하기가 어렵다.
불순도와 엔트로피(Entropy)는 비례관계라고 할 수 있다.
이 엔트로피 지수는 의사결정나무(Decision Tree)에서 해석을 하는데 중요한 용도로 사용된다.
의사결정나무(Decision Tree) 모델은 각 노드의 순도(Homogeneity)가 증가하거나 불순도(Impurity) 또는 불확실성(Uncertainty)이 감소하도록 하는 방향으로 학습을 진행한다. 따라서, 이 학습 진행 방법으로 사용되는 것이 바로 엔트로피(Entropy)다. 이 엔트로피(Entropy)를 이용하여 정보획득량(Information Gain)을 구하게 된다.
정보획득량(Information Gain)은 의사결정나무(Decision Tree)에서 아래의 식을 이용하여 구하게 된다.
정보획득량(Informaiton Gain) = 분할 전 엔트로피(Entropy) - 분할 후 엔트로피(Entropy)
정보획득량(Information Gain)이 크면 불순도가 줄어든다는 것을 의미하며, 정보획득량(Information Gain)을 계산하여 값이 가장 큰 속성부터 기준을 삼아 의사결정나무(Decision Tree)에서 분할을 하게 된다.
의사결정나무(Decision Tree)를 효과적으로 배치하는 방법은 앞 노드들의 엔트로피(Entropy) 합계를 최소화하고, 정보획득량(Information Gain)을 최대화할 수 있는 속성을 순서대로 배치하는 것이 중요하다.
'빅데이터 분석 > 빅데이터 분석 학습' 카테고리의 다른 글
| [데이터 크롤링] 서울 약국 경위도 크롤링하기 with Python (0) | 2021.05.25 |
|---|---|
| [데이터 크롤링] 서울 카페 경위도 크롤링하기 with Python (0) | 2021.05.25 |
| [Python 크롤링] 네이버 뉴스 크롤링하기 with Python (0) | 2021.05.24 |
| [데이터 크롤링] 카카오 api를 활용한 서울 편의점 경위도 크롤링하기 with Python (62) | 2021.05.21 |
| 파이썬 크롤링을 이용한 주식매매동향 간략한 데이터 분석 (1) | 2020.11.28 |
| 인포그래픽과 빅데이터 시각화의 차이 (0) | 2020.09.09 |
| 통계 일변량 분석 기초 (0) | 2020.08.27 |
| 빅데이터 분석과 데이터베이스 이론 (0) | 2020.08.25 |









최근댓글